|
||||||||
|
|
||||||||
Sword
Motions and Impacts
An Investigation and Analysis
By George Turner
ARMA is generally skeptical of attempts to quantify swordsmanship from an engineering or physics point of view, as we feel the craft is more of a holistic one. But occasionally we are impressed by insightful technical analysis and in this case, especially so. The following enlightening article presents for the first time material which contradicts some of the long held assumptions about the physical mechanics of swords. Understanding the function of swords is about understanding their design. This is a matter of understanding the complex elements of blade geometry. Yet, these are little understood today, even among many commercial and private sword manufactures. A sword cannot be examined solely from a silhouette or face on view. It must be examined based upon its whole blade profile - overall shape, length, width, and differences in thickness and taper in its cross-sectional change. There are even variations in the stiffness of different blades designed for cutting at different materials, or those for cutting and thrusting use, and those designed for thrusting only (and even then, there are differences between soft versus hard targets). These are some of the reasons why one sword will feel good and another won't. But few individuals have had opportunity to closely examine or measure a wide range of authentic antique pieces to know their subtleties. Elements of balance, flexibility, and weight in a cutting sword are very subtle. On top of this, just as there are considerable misconceptions about how swords are used, so there are also about how they mechanically function as tools. How all this relates to understanding the actual function and handling of cutting swords will in turn reflect how a maker produces his modern replica weapon and what today's enthusiast looks for in a blade. It also underscores the importance of experience in actually hitting at substantial test-targets with sharps blades. As George Turner now shows here, the majority of sword makers have unfortunately been talking utter nonsense for the most part with nearly all of their pronouncements on the factors of how good swords function. George's research amounts to no less than a revolution in sword theory, but as he demonstrates it really only reveals what was already known long ago. In the process he also manages to vindicate some of ARMA's long held complaints on the failures of modern sword reproductions. As a result of this article, while the making of a fine sword will surely always remain an art, we can now safely say it's one firmly grounded in science --"the sword mystics are doomed."
Part I
Background
Since first joining ARMA in 2000, I’ve been talking with Director John Clements about problems encountered with modern reproduction swords. This has made me very interested in the dynamics of impact weapons, and I ended up conducting investigations in this area, bouncing all kinds of ideas off John and many other members and colleagues. Though not yet completed, some very interesting things have come out of it. The part of the analysis presented here mostly concerns the rigid body motions, which occur both during a swing and as the result of an impact. The principles should be nothing new to physicists and engineers, though it’s probably much simpler than many might expect. I’ve simplified this material as much as possible for a general audience, to avoid inflicting assorted equations on readers. [Also, while an effective sword cut needs proper body mechanics and grip behind it to insure ideal edge placement and focus, for sake of argument these elements are assumed to be at work here when discussing blows].
During impact of a sword cut, the sword and target undergo what Aristotle referred to as violent motion, as distinguished from what he called natural motion, and this motion causes a rapid change in the linear and angular velocities of the sword. If you compare the post-impact motion of a sword with the pre-impact motion, you’ll see that the sword pivots around a point that is generally somewhere on the handle. This pivot point isn’t fixed in space, as if it was nailed to the ground, but rather is a point whose linear motion is unaffected by the impact. The location of this pivot point varies, depending on the impact’s location on the blade. But it doesn’t depend much on the velocity of impact, or any other such measure. Since for any particular impact point the pivot location is fixed, the resulting change in motion of the sword must be in the arc of a circle, and the pivot point is at the center of this circular motion. All hand held rotational impact weapons behave in this way, as do all objects in general (ed. Giacomo Di Grassi in his 1570 fencing treatise first described the motion of a sword cut in terms of circular motion).
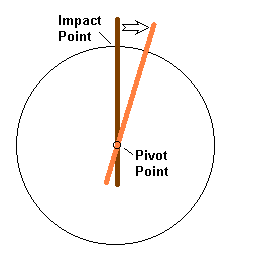
Figure 1 - Diagram of an Impact
When you take a staff and make an impact at a particular point on the shaft, the staff pivots around another point. The impact point and the resulting pivot point are of course always on opposite sides of the staff’s balance point. For an untapered staff, if you make an impact inside the middle third of the staff, it pivots around a point in space that’s past the end of the staff. If you make an impact directly on the staff’s balance point, it doesn’t seem to pivot at all, as if the pivot point is infinitely far away. However, if you impact exactly one third of the staff’s length from the tip, the staff pivots exactly around the butt end. If you make an impact on the tip, it pivots one-third from the butt end. If you impact exactly one forth from the tip, the staff pivots one sixth from the butt end.
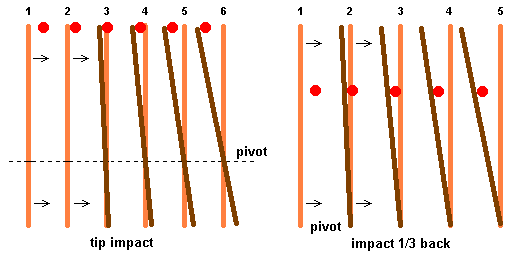
Figure 2 - Staff impacts with staff moving linearly to the
right.
As shown in figure 2, the staff pivots relative to where it would have been, if there hadn't been contact with the target. In the illustration, the lighter staff misses, and stays on its original course. The darker staff makes contact with a target, and pivots at a point that's fixed in relation to the staff that missed. Suppose you swung two swords at a target, both held parallel and side-by-side. If one sword hits the target, and one sword misses it, the swords will act like a pair of scissors during the impact. But the point of impact on the blade determines the location of the connecting pin. So you could say that a swing has two possible futures. In one future the swing misses the target, and the sword continues around in its natural path, just as it does during flourishes. In the other future, it impacts the target at some point on the blade. The pivot point is the part of the sword that generally follows the same path in both timelines, but this occurs only as long as the sword is in contact with the target, as in figure 2. To a hand at the pivot point, hitting and missing are the same.
These pivot points also appear when the weapon is in rotation, and the position of them is the same as with linear motion. The following illustration is the same as the previous one, including the use of two staffs to illustrate the change in motion, but the staffs were already rotating when one collided with the target.
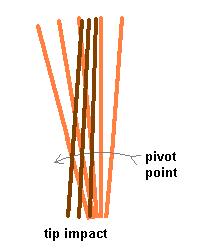
Figure 3 - Tip impact with the staff in rotation.
As shown in the above illustration, the two staffs were sweeping around toward the left, but the tip of the darker staff collided with the target. The path of the light staff doesn't make any sudden changes in motion, while the motion of the dark staff undergoes sudden and drastic alteration. A hand placed anywhere on the light staff wouldn't feel any shocks. A hand placed on the dark staff, but at the natural pivot point, also wouldn't feel any shocks, since the pivot point roughly follows the same trajectory for both staffs. But a hand on the dark staff, far from the pivot point, would feel the forces from the suddenly altered motion. Basically, in this case the hand must speed up to stay with the staff, and to accelerate an object requires applied forces. But in accelerating the hand, the butt of the staff would also be slowed, so don't necessarily think that the hand is forced to follow the geometry. An external body, like the hand, if affected by the staffs change in motion, must likewise also have an effect on that change in motion.
A quick way to feel how these pivot points work during an impact is just to grab a staff and start hitting things. Notice that if your hand is inside the natural pivot point of the impact, which is again just the center of the arc of the resultant motion, it will be knocked forwards. In figure 3 this would occur if you’re holding the butt end of the staff, and make an impact with the tip, as happens in the illustration. Your hand is then on the darker staff, and ends up forward of where it normally would’ve been. You feel this as a kick into your fingers. If you instead make an impact far back on the staff, so that it pivots near the butt end, or even past the butt end, then your hand is slowed or stopped by the impact. You feel this as a kick into your palms or directly into your wrists.
Another way to think about this is in terms of your hand’s natural pivot point. If you strike a blow and the handle kicks into your fingers, you’ve hit out past the point that would make your hand the center of the impact. If you strike a blow and the handle kicks into your wrist, you’ve hit inside the point that would cause the weapon to pivot around your hand. By making a succession of blows, and paying attention to the kick at a particular finger, you can quickly find the desired impact point on the blade.
By measuring these impact and pivot point locations, and finding their distance from the staff’s balance point, a surprising bit of geometry emerges. Draw a rectangle extending from the staff’s balance point, with one side extending to the impact point, and the other side long enough to reach the center of the impact’s resultant motion, or pivot point. If you do this for several pairs of impact points and pivot points, you’ll find that the rectangles all have equal areas. For the staff, this area is one twelfth of the square of the staff length. In general, this means that the two distances, taken from an objects balance point to the impact and pivot points, when multiplied together, form a constant. Handily, this means you can just measure one impact point and the resulting pivot point, find the area of the rectangle, and from this rectangle find the pivot point for any given impact point with just simple geometry.
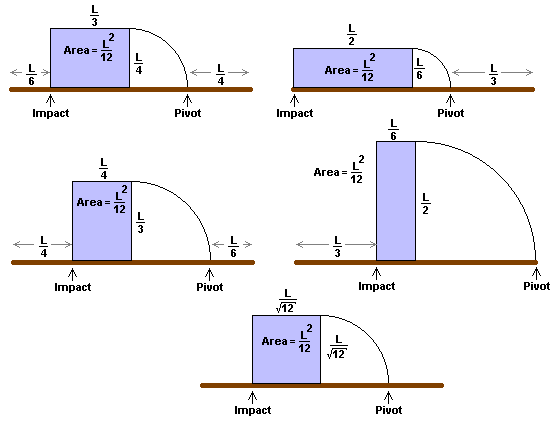
In the figure above, you can see these rectangles for a collection of impact points and corresponding pivot points. Once you know the area of just one rectangle, for a given weapon, you also know the area of all such rectangles. This also lets you use geometry to gain some simple insights. One problem is to find the shortest distance between an impact point and pivot point, for a given weapon. The geometry shows that this is just a problem of finding the rectangle with the smallest perimeter, which encloses the given area. This is of course a square, which is shown at the bottom of figure 4. This also guarantees that for the shortest distance between an impact point and pivot point, both must be equidistant from the balance point, which is true for all weapons.
You should also realize that if one side of the rectangle gets very small, the other must get very large, just to maintain the area of the rectangle. This means that you can’t make the pivot point very close to a weapon’s center of mass, since it would mean the corresponding impact point would move past the end of the weapon. Since an impact can’t actually occur past the end of the weapon, there can’t be an impact that produces a pivot point that’s very close to the weapon’s balance point.
There’s another handy way to find these points on a staff, which doesn’t involve impact, and which is very useful if you start doing any modifications to the staff, such as tapering the ends or adding a spear point. Just take the staff in hand and hold it vertically by very lightly gripping it with your thumb and finger. Then shift your hand around and watch the staff pivot around a point somewhere near the top end. Gravity will mess with the test a bit, which limits its accuracy, as will any actual torque you apply with your hand. Don’t wave the staff around like a wand, act like your trying to do a crazy staff-balancing trick at a party.
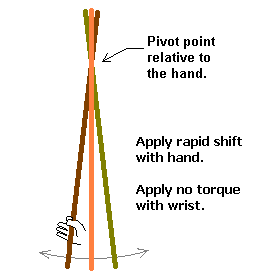
Figure 5 - The waggle test for a staff
The key to these tests is that you don't apply any torque. If you only apply side forces, which act like the forces from an impact, the staff will rotate around its natural pivot point, relative to your hand's location. A slightly better form of the staff test is to balance the end of the staff on your open palm, which certainly can't apply any torque to the shaft. This test also works well for swords, but you lay the cross across you thumb and forefinger, which also virtually guarantees that you're not adding any torque, since you're not actually gripping anything.
Another way to guarantee that you don’t apply any torque while performing a “waggle’ test is to apply the sideward forces with a string, since strings don’t normally transmit any torque. All a string can do is pull, so if you use a string to move the hilt, you can’t be applying wrist torque. But knowing this brings up another interesting observation. Since the pivot point doesn’t move when the forces are applied at the impact point, it isn’t feeling any tangential forces. If there were an unbalanced force on the pivot, it would accelerate, which would change its velocity, and that doesn’t happen. Similarly, when you perform a “waggle” test, the reason the test works is that your hand can’t move the pivot point without using wrist torque. An impact point and its corresponding pivot point can’t apply torque to each other. Since the impact point and pivot point can’t apply torque to each other, the two points behave as if a string connected them. If the two points were in fact just connected by a string, the observed effect would be the same, pushing sideways on one point wouldn’t affect the velocity of the other point.
So if we were interested in finding the location of the impact point that causes the sword to pivot around the cross, we could first do the simple waggle test, with the sword’s cross balanced on our fingers, which would give an approximate location for the required impact point. Then we could take a string, tie one end to the cross, and the other end to a weight, and carefully adjust the length of the string, so the weight is positioned exactly adjacent to the proposed impact point. Then we could swing the sword around by using another cord, also tied to the cross, just to make sure we don’t apply any wrist torque. If our guess at the impact point is correct, meaning our string is the right length, then however we swing the sword, the blade and the weight will be inseparable. If the string is too short, the weight will try to race ahead of the sword. If the string is to long the weight will lag behind the blade. By adjusting the length of the string, and observing whether the blade or weight comes around faster, you can find the exact location of the impact point that will make the sword pivot around the cross. And as I’ve shown, once you know the locations of one impact point and pivot point pair, you can easily calculate any of them.
Figure 6 - A saber with plumb bob. The bob keeps time with the blade.
Not only do they stay together as you sling them around, they also stay together when you hang the sword by the cross and set it swinging. As always, the sword and the plumb bob will swing together, and a swinging plumb bob is nothing but a simple pendulum. You can even mount and swing the bob separately, since the period of the pendulum depends only on the length of the string, so it doesn't have to be physically attached to the sword.
There is an ancient weapon that illuminates the rotational behavior of a simple pendulum, called the sling, which has two chords attached to a pouch containing a rock. The sling is whirled in a circle until it's up to speed, then one string is released and the rock flies out. All the forces involved are transmitted in tension, along the two chords, always in a direct line between the rock and the hand. The nice design feature of a sling is that the string doesn't allow any torque to be applied to the pouch, because a sideward force on the pouch might make the rock fall out. By using a string to connect the pouch to the hand, the only forces on the rock are guaranteed to be in line with the string, acting directly toward the hand. Similarly, during a sword impact, if there were a rock attached at the impact's natural pivot point, it would stay put, since there isn't any change in sideward motion at the pivot point.
An interesting thing about slings is that the longer the string, the harder it is to get the rock moving. With a short sling you can get it up to speed almost instantly, just by whirling your hand in a small circle. With a very long sling, you have to make slow circles with your whole arm, since the long sling responds slowly, and has very little tendency to rotate around on its own. The same thing happens with swords, though not based on their length. The tendency for a sword to naturally rotate around is based on the distance from your hand to the natural pivot point relative to your hand. This is the point where the plumb bob swings in equal time with the sword, and it is the length of this pendulum that lets you relate how a sword swings to how a sling rotates. You might refer to the length of this pendulum as the natural length of the sword, as opposed to its true length. Consider that if you make a sling that reaches from your hand to your sword's natural pivot point, and swing them both together, the rock will stay adjacent to the blade. This means that two points on the sling, the rock and the hand, stay even with two points on the blade, which means the blade must be moving exactly like the sling, and be moving according to the true length of the sling, which is the distance from the hand to the hand's natural pivot point.
For a hand traveling at constant velocity, and in a purely circular arc, the angle that your hand must pass through before the sling catches up, recovering from any initial displacement, is a function of the square root of the length of the sling. This is the same as a pendulum's frequency not depending on the initial displacement, as long as the displacement isn't extremely large. The same applies to a sword swung without wrist torque. It doesn't matter how far the sword is initially cocked, or how fast you move your hands. A short sword might always realign itself after 70 degrees of uniform hand travel, whereas a longer sword might take 90 degrees. However, this simplistic approach just reveals the general behavior, as your hand is actually accelerating, not traveling in a perfectly circular path, and applying tremendous torque to bring the blade around. But the distance between your hand and your hand's natural pivot point will always affect the way the sword swings.
But the previous discussion on the pivot points of a staff showed that the distance between pivot points varies widely, growing very large as one of them approaches the center of mass. Unlike a staff, we generally grip a sword very close to the balance point. And when you grip a staff very close to the balance point, the resulting pivot point is very far away. If you grip a staff in the middle, as if you were going to throw it like a spear, it doesn't want to rotate at all. We've all complained about swords that don't swing well, because they were balanced too far back. This is the real reason why. The balance point is very close to the hand, so the corresponding pivot point is very far away, far past the sword's tip. It is the same as trying to swing a spear while gripping it for a throw, or swinging a very long sling.
The way mass is distributed throughout the object determines the location of the pivot points. When you apply force to a staff, such as with an impact, the force does two things. It accelerates the object's center of mass in a linear fashion, since, as we all know, force equals the mass times the acceleration. But the force also serves to rotate the object, because it is also applying a torque. Whereas the object's center of mass accelerates according to the force divided by the mass, the object rotates with an angular acceleration given by the applied torque divided by the objects moment of inertia, taken about the center of mass. The combination of these two motions determines the location of the pivot point for the resulting motion.
If you taper a staff, all the pairs of pivot points start moving in toward the center. Basically, adding mass to the middle, or shaving mass from the ends, decrease the total area of those rectangles. This means that when you taper the mass, yet leave the balance point unchanged, the area of the rectangle gets smaller, but the corner that touches the weapon's balance point doesn't move. So for a particular impact point, the distance to the weapon's balance point is unaffected, which makes up one side of the rectangle, and since the rectangle is smaller, then the other side of the rectangle must get proportionally smaller. What's happening is that the weapon is becoming proportionally easier to rotate than to accelerate, so it starts pivoting closer to the balance point.
Another interesting thing is the behavior of these pivot points when you add a lump of mass somewhere, like a pommel or cross. For an impact that causes the weapon's change in motion to be centered at the pommel, the pommel isn't really doing anything to affect the impact, since it's just spinning around its center. So, whether the pommel was there or not wouldn't affect the resulting motions. Similarly, if you're pushing back and forth on the pommel, to see where the resulting rotation is, the pommel could just as well be separately held in your hand. The resulting forces and motions are the same. So adding a mass has little or no effect on the impact point relative to the added mass. Thus the cross has little effect on the pivot point relative to the cross, and a pommel has little effect on the location of the pivot point relative to the pommel.
But added mass can drastically alter the location of pairs of pivot points located elsewhere. For pivot points in between the added mass and the new balance point, the relative impact points are moved outward. Take a cavalry saber, which has a pivot point at the forefinger that results from an impact a third back from the tip. When you add a pommel, the forefinger will have a respective impact point that moves much closer to the tip. Simple math says that it's physically impossible for this not to happen. When you add a pommel, you're pulling the balance point closer to your hand. The pommel is to some degree changing the area of the rectangle that describes the sword, but more importantly, it's squeezing the side formed from your forefinger to the balance point. Squeezing the short side of the rectangle makes the other side get much longer. Basically, the long side gets longer much more than the short side gets shortened, just to preserve the area of the rectangle.
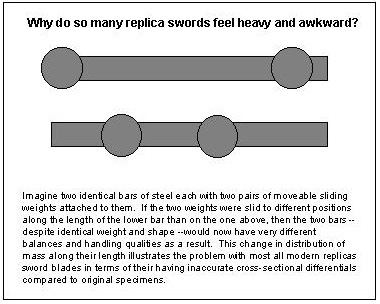Interestingly,
the sizes of the pommels we find on authentic swords indicate that the result
must be a pivot point very near the tip. So swords with real pommels must behave
quite differently from cavalry sabers. Using an overly large pommel would move
the pivot point past the tip, which would guarantee that no physical part of
the blade could ever be used for an impact that doesn't cause hand shock. In
addition, a pivot point far past the tip would make the sword rotate very poorly,
like an extremely long and unwieldy sling. So the existence of extra large pommels
is doubtful. Likewise, if the desired pivot point was anywhere near one third
back from the tip, why use a pommel at all? Just leave it off and have the sword
pivot around a point about a third back from the tip, just like a saber. So
I would say that if a sword has a real pommel, it would only logically be used
to create a pivot point very near the tip.
Suppose that the desired pivot point is exactly at the tip, and go back to the drawings of rectangles, where we can quickly see just how sensitive a sword is to the location of the balance point, which is set by the size of the pommel. If you have a 45-inch blade, with a balance point 5 inches forward of the cross, and a natural pivot point, relative to the cross, located at the sword's tip, you'll have a 5x40 inch rectangle, with an area of 200 square inches. Note that the rectangle is already eight times taller than it is wide. If you add a large pommel to pull the balance point back to 4 inches, then you've squeezed the sides of the rectangle, making it much taller, and the pivot point moves 9 inches past the tip. If you pull the balance point back to 3 inches, the pivot point moves more than two feet past the end of the tip. You can buy swords like this from some of our best manufacturers, so don't think it can't happen. This is all the result of the mistaken notion that the pommel is there for balance, which is all that Sir Richard Burton, and many others, could figure out. I would argue that the pommel was used to control the sword's rotational behavior, pure and simple [ed. and also to prevent the hand slipping off during certain tehniques]. Maybe the early sword researchers should've asked why a short sword needs a pommel for balance, while a heavy, forty-five inch cavalry saber does perfectly well without one.
To find out where authentic swords place this natural pivot point, I did some very simple waggle testing with several 16th century swords in a private collection, while attending a recent ARMA retreat. I already had some accurate data from six reproduction swords, from some of the best modern manufacturers, and their pivot points, relative to the cross, vary anywhere from 10 inches behind the tip to 20 inches past the tip. Oddly, all of these authentic swords pivoted within about an inch and a half of the tip, which is also close to the accuracy limit of my simple waggle test. Considering that the odds of any one particular sword doing this are about one in twenty, given the similar sampling of reproduction swords, the simplistic odds of six in a row doing this are one in sixty-four million. So it seems that the people making the authentic swords were probably paying pretty close attention to this rotational behavior, and carefully controlling the location of the sword's pivot point, which apparently is a trick that was lost far in the past.
|
|
|||
|
|
|||
|
|||