|
||||||||
|
|
||||||||
Once you start making hard and sharp impacts near the tip of a straight sword, some other interesting physics comes into play. The first thing you'll notice is that your handle either bends or even breaks off. The reason this happens is again due to the pivot points of a sword. When making impacts about a third back from the tip, the impact point causes the sword to pivot around a point that was very close to the pommel. These impacts, having the change in motion centered near the pommel, don't actually change the pommel velocity by any significant degree. The tang (the inner 'tongue' of the blade inside the handle) really doesn't encounter any significant forces during these types of blows, but simply has to pivot around the pommel.
Figure 15 – A mid-blade impact point causes the sword to pivot around the pommel, causing little or no stress on the tang.
But as you start hitting near the tip, or directly on the tip, the sword pivots around the cross. This means that the pommel is far away from the pivot point, on the other side of the fulcrum, and has to make a large and sudden change in velocity. The tang is the only thing that actually delivers the forces necessary to accelerate the pommel. Since the pommel is heavy, it resists this acceleration, so the tang really has some work to do, and only a very brief amount of time to do it, because of the violent nature of an impact. In a typical high-speed impact, say 75 miles per hour, the pommel might have to change velocity by 15 mph or more, depending on hilt length. If the blade and tang are stiff, the pommel will need to change its position by ¼ inch in just one millisecond.
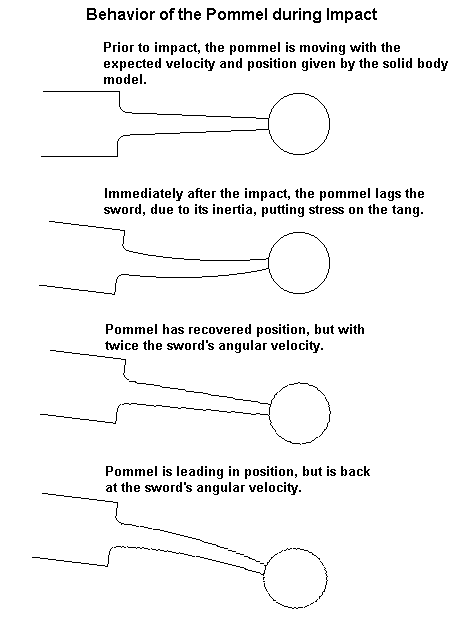
Figure 14 - Simplified diagram of tang motions during impact.
An end-loaded cantilever beam is a good approximation for the tang and pommel system, and this just forms a spring mass oscillator, with the mass at the end of the spring. For those who didn’t major in mechanical or civil engineering, a cantilever is just a beam that has one end stuck in a solid wall, and the other end free. A flagpole sticking out horizontally from a building is a good example of a cantilever beam. The tang and pommel, acting like a cantilever beam, just forms an oscillator, a bit like a tuning fork. It is very possible that a sharp high-speed impact will excite it in under a quarter of its natural period, where the change in kinetic energy of the pommel must be momentarily stored in the tang. This is similar to the behavior of a hanging pendulum when you strike the bottom. The kinetic energy in the bob will get converted to potential energy as the bob reaches the apex of the swing, and then it converts the potential energy back to kinetic energy, as the bob moves back through the bottom of the swing. The only way the tang can store this energy is by bending, storing strain energy that must later be converted into the kinetic energy of the pommel. From the tang’s perspective, fixed to the blade, the impact looks like the pommel just suddenly started traveling at a very high velocity, which is the initial impulse that starts the oscillator.
To calculate what the maximum necessary strain energy might be, you have to know the change in kinetic energy of the pommel, which is a pretty trivial calculation. Since a tip impact is centered on the cross, simple geometry will tell you that the change in pommel velocity is at worst just the change in tip velocity, multiplied by the ratio of hilt length to blade length. If you strike an unyielding target, then the change in tip velocity is the same as the swing velocity. You then use some simple formulas for the energy stored in a cantilever beam, which gives a good description of the tang, you come up with some numbers that are a bit frightening. For reasonable estimates of historical tang sizes, pommel masses, and tip velocities, the tang might be operating very near the yield strength of the steel. In a tip impact at 75 miles per hour the pommel might have to change velocity by 15 mph or more, depending on hilt length. If the blade and tang are stiff, the pommel will need to change its position by ¼ inch in just one millisecond. To accelerate a typical pommel at this rate requires literally hundreds of pounds of force. The key to making the tang survive these forces are an adequate cross-sectional area at the cross, a taper ratio that doesn’t allow for shear failure near the pommel, and either making sure the steel is spring tempered, just like the rest of the blade, or allowing extra cross-section and a milder temper. The problem is exactly the same as the type that’s encountered in the design of crossbows and siege engines. Basically, if you put the sword in a vice, you need to be able to use the tang like a pommel flinger, and if it can’t accelerate the pommel to the velocity that will be encountered as a result of real impacts, then it will likely fail. But it is also helpful if the pommel is very stiff, because this keeps the tang from damping the pommel’s contributions to the impact forces. Of course this means that you'll need a winch to crank the tang back and fling the pommel, so maybe analytical methods would be better.
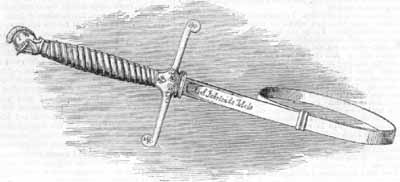
Figure 17 – A tang on an authentic sword. If the Lockheed Skunk Works designed a tang, it would probably look much like this.
It is no wonder that ARMA students have so many tang failures on replica swords, since we teach to forcibly strike with the weak, instead of the mythical point that’s one third back from the tip. Hard impacts with the tip induce very high bending stresses in the tang, which is why some reproduction swords might not tolerate it, since no one seems to have thought of this potential problem, at least not in the last hundred years or so. However, all this also tells us that tangs shouldn’t necessarily be left soft. The tang operates under just as much stress as the blade, if not more so, and great care should be taken in its design and heat treatment. The part of the tang that should be left truly soft is just the very tip, which after tempering can be pushed against a hot piece of steel and allowed to slowly cool.
Just keep in mind that the cross-sectional area of the tang is critical, as
is the safe working stress of the steel, but squared. If you drop the tang steel’s
yield strength in half, you need four times the cross-sectional area in the
tang. Some of this work needs to be pursued much further, but at least we’re
getting to a standard engineering question, which can be easily addressed. In
the mean time, be very careful of hard, high-speed tip impacts with existing
reproduction swords. Even if your sword can take it, someone else’s might
not. Right now, we don’t know which swords will survive this kind of violence,
and even the ones that do survive might be forming incipent stress cracks or
moving toward fatigue failure. Unexpected and total tang failure is one of the
nastiest failure modes for a sword, and we don’t want to see it happen.
Considering
the importance of tang flex, one might wonder whether blade flex is of much,
much greater importance. Interestingly, the answer is no. Vibration does come
into play, but is not the dominant mode of energy loss in a fairly clean cut.
Much of the sword's initial energy is retained in the slower, but still significant,
post-impact velocity of the sword. Much of the rest of the energy is dissipated
in the actual cut. The energy feeding into vibrations will vary widely, based
on how hard the impact was, where it was, and obliquity. Note that an oblique
cut not only tends to dump energy into the side-to-side oscillations, but will
also cause the apparent blade cross section to be sideward. This means the blade
is trying to cut on a slant, which builds up much higher target resistance.
This puts higher deceleration forces on the blade, which will increase the flexture
forces in both the edge-to-edge and side-to-side planes.
I've argued that the desired edge impact point on a real sword is probably closer to the tip, and for this type of impact the flex will be better represented by a cantilever beam model, which is loaded near the end. If you strike with the tip of a foil, the tip obviously bends to such a degree that no large impact forces are generated, and the energy in the blade largely gets converted to strain energy, which stays in the blade until released. Basically, the impact model changes from being similar to a person falling out of a window and onto the sidewalk, which makes a splat, into the same person landing on a trampoline. But the same logic also says that if you stiffen the object, the basic pattern oscillations still exist, but they don't matter as much. The top level of a parking garage still has complex patterns of oscillation, just like the trampoline, but the increased stiffness makes trampoline dynamics less important, and you'd still go splat during an impact. So as you go from a very flexible object to a very stiff one, the vibration energy goes from a dominant role to a minor one. How much it matters to a particular sword depends on the sword's flexibility.
Another way to look at the switch model is that if flexing means that the blade and target didn't make a solid collision, there is less impulse being transferred, at least in the early stages of the collision. Given that impulse is just the change in momentum of both sword and target, and always applied equally to both, this means that the target didn't speed up very much, nor did the sword slow down. If you strike a blow and neither the sword nor target change speeds to a significant degree, then something interesting is happening. The target and the line that marks the axial center of balance of the sword must overlap, and since both are made up of solids, this means that the sword is bending to such a degree that the line describing its center actually moves past the target, which is a pretty good description of the impact of a switch or a foil, which bend around the target, instead of striking a solid blow. Wide cutting swords just don't bend to nearly this degree, and a good cutting sword won't wrap around a target. The two edges are far apart on a wide blade, and for the sword to significantly bend in this plane the edges would have to stretch by a huge amount. Sword edges just can't stretch that much.
Whereas the tang model requires that the change in kinetic energy in the pommel might momentarily be stored entirely as strain energy in the tang, the blade impact model doesn't necessarily require this. If this were the case, the blade would always have to temporarily store all the impact energy. The pommel is very solidly connected to the tang, and the forces in between the pommel and tang can grow to such a magnitude that the tang suffers bending or shear failure. If you make your tang very stiff, then the forces are extremely large, but the displacement is small. Whereas if you keep the same cross-sectional area, but make the tang very narrow, the forces are small, but the tang bends through a large distance, as if it was the limb of a crossbow.
With the sword blade, the impact forces aren't distributed over the large contact area shared by the tang's connections to the pommel. In fact, the blade area presented to the target is made as small as possible, so that the sword will cut. This maximizes the amount of pressure applied to the target for a given amount of force. This is why edges are thin and sharp. Against a target that is subject to cutting, this means that there is a limit to how high the impact forces can build, before the target gets cut by the blade. If we assume that there is some standard target behavior, such as a bare arm, or one wrapped in cloth, or even armored to some degree, then the result is the same. The impact forces will reach some limit that either causes cutting or denting. In the absence of this limit, such as when trying to cut an anvil, I agree that the swing energy will largely be converted into strain energy and thus vibrational energy. But given a target that can be cut (or dented), there is a maximum level of impact forces, determined by many factors, especially the properties of the target and the cross-sectional shape and sharpness of the blade.
Given some limited amount of force, and noting that this force is applied at the end of the cantilever beam, this means there is a maximum bending moment on the beam. So now we come to an equation describing the energy stored in a cantilever beam when under the application of a fixed load. The dynamic results of this are a hairball, which to this day often can't quite be exactly solved. But we just need a trend, not an exact solution. In the equation for stored strain energy, the stiffness of the beam appears in the denominator, which will limit the amount of vibrational energy in the impact models. Unlike a foil, or a switch, which are very flexible, real swords are wildly inflexible when stressed along the edge. If you have a blade with a diamond cross-section that's 3/16 inch thick and 1-7/8 inches broad, then it is one hundred times stiffer in the edge-to-edge plane than the side-to-side plane. This means that under equal end loadings, alternately applied to the edge and side, the stored strain energy in the edge impact is only one percent of the strain energy that could be stored during a side impact. Since the vibrational energy is directly related to the strain energy, stiffening the blade keeps the impact forces from feeding significant energy into vibrations.
If you watch a person on a diving board, you can see the board store the strain energy, bending in the fundamental mode, and then using this stored energy to propel the diver. But if you rotate the diving board so the diver is standing on the edge, then there is almost no deflection, and thus no stored energy. The diving board then acts like a solid surface, which is why floor joists are oriented vertically, instead of on their sides. For a given load, if this vertical orientation stored as much strain energy as the horizontal orientation, then we'd all barely have the strength to walk across a room, since the floor would be damping our efforts. This is why a car's suspension uses leaf springs, instead of I-beams. It shouldn't be too difficult to actually measure the energy in the side-to-side oscillations on a particular sword, since you should be able to drop a ball bearing onto the blade, and from the bounce height determine how much missing potential energy to account for. From the amplitude of the resulting oscillations, roughly calculating the energy levels in other amplitudes shouldn't be very difficult.
Given that strain and vibrational energy are a significant component of foil impact dynamics, but are reduced by around a hundred fold in a similar sword impact, I'll argue that they aren't generally a significant component of sword impact behavior, at least against softer targets. Basically, by reducing an important component of the energy to around one percent of its previous value, the tiny amount that's left becomes much less important, since we can't swing a sword to that level of precision. Even if the vibrational energy were all of the energy in a foil impact, this would still mean that it's only a small percentage of a cutting sword's impact energy. When you make the sword blade very wide, and thus very rigid, it starts acting like a rigid body, and its behavior is better explained with the rigid-body impact model. The conventional approach in other areas of impact dynamics is to lay the flex and vibration model on top of the rigid body model, to account for a more complete description of the dynamics. Remember, a cutting blade's function is to cut and enter into bodies, and when cutting through flesh there's no serious and complex high-frequency vibration going on near the impact zone, because strong contact with a soft material damps vibrations. This is why you silence a musical instrument, such as a bell, by putting it in contact with your hand. However this is different from the way you use your hand to silence a bad musician. For that technique you need to read the works of Fiore, Vadi, or other masters.
As for the side-to-side oscillations that some are so fascinated with, I would likewise not let them dominate the analysis. The energy in a mechanical shear wave goes up with the square of the amplitude, so a wave with a 20-inch peak-to-peak amplitude has 100 times the energy of a 2-inch wave. Since a static deflection against a full strength blow can easily make the sword flex and flap in the 20 to 30 inch range, those little 2 or 3-inch oscillations left in the blade after a normal impact can only account for a tiny percent of the impact energy. Not till the oscillations become much larger, probably in the 6 to 9 inch range, would they start containing more than about 10% of the original swing energy. Remember that we're dealing with a square law, so that slight wobbles have very little energy, but the energy grows quickly as the wobbles start becoming really large.
There's also the problem about the location of the node of oscillation. When the sword is freely oscillating, the node is about a third back from the tip. However, in a hard impact its location shifts to the impact point. The reason for this is the same as the reason you always find a node of oscillation under a guitarist's finger. The finger makes the node by not allowing the string under the finger to move. Similarly, a hard contact fixes one location on the blade, making the rest of the blade's vibrations conform to this contact. So the location of the node of oscillation is always about a third back from the tip, except during a hard impact, which is the only time it would matter anyway.
Also note that supposed hand shock is very different from mere vibrations. If you've driven a car with a front tire slightly out of balance, you've probably noticed your hand vibrating an eighth of an inch or more, making it just a blur on the steering wheel. But this doesn't hurt, or make you cry out, at least not for the first 50 miles. Sometimes you don't even notice the vibration till you look at your hand. Similarly, when you apply a wrench to a running engine, you may have trouble getting the wrench on the bolt, but you won't hurt your wrist. The edge-to-edge vibrations are probably in the right frequency band to inflict some pain, which is about 50-300 Hertz, but the blade is too stiff, edge-to-edge, for the amplitude of these vibrations to get very large. Basically, by the time the vibration starts squishing tissue, it has to reverse and head the other way. If you're completely uncomfortable with the vibration in your hands during swordplay, try strengthening your arms, or try a different sword, or even take up a different pursuit. Violent jesting with sharp-edged tools isn't everyone's cup of tea.
The side-to-side vibrations are even less likely to explain hand
shock. The wave velocity is also not fast enough to reach your hand in time
with the impact. If you slap your blade, you can time how many oscillations
it's making in a second. Then measure the distance between your two nodes, which
is half of the wavelength of the oscillations. Multiply the frequency by the
wavelength and you get the travel velocity of a mechanical shear wave traveling
side-to-side down your blade. The side-to-side waves actually travel very slowly,
and you'll likely be starting your next move before the side-to-side waves from
the previous impact finally reach your hands. To sum this up, when a bus hits
you, it's not the bumper's vibrations that do the damage. It's the impact.
We’ve all heard about the power of a draw cut. Some even believe that only a draw cut can hurt an opponent. I think this comes from a synthesis of 19th century writings combined with some concepts from Asian arts, and also perhaps a misreading of Di Grassi's instructions to pull the blade upon impact of an edge blow after you first make a full circumference of your arm from the shoulder. Though the famous hoplologist, Sir Richard Burton, in his 1884, Book of the Sword, argued that the drawn cut moves the edge through the target at a very shallow angle, he wildly exaggerated the effects. He also completely misunderstood the geometry, with illustrations of cutting that aren’t physically possible, and ended up with compounded errors.
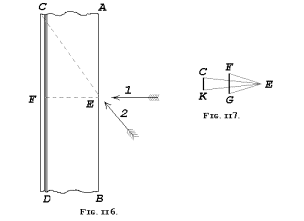
Figure 15 - Burton's illustration of cutting angles (The Book of the Sword, p. 130)
As the above figure shows, he not only thought that cutting straight across the blade makes for a shorter distance, but also a much thicker blade. This isn't just an error by the illustrator, since it's explained in the text. For those of you who like to use micrometers to measure your blades, keep in mind that his sword theory can cause the spine to magically thicken by huge amounts, as shown in his Figure 117. Note that in truth, the lines C-K and F-G must be exactly equal, unlike what he shows. Geometry can correct the exaggeration, as shown here.
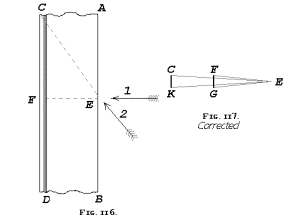
Figure 16 - A trivial correction of Burton's geometry.
However, the corrections aren’t complete. Sword blades reach very high velocities. Even the end of a baseball bat travels at over 77 mph, and that’s just in a standard college level swing. Some of our sword swings should exceed this by quite a bit, because they’re longer and less tip-heavy. So in a hard swing, you’d better be able to make good contact with the taillights of a car that’s traveling at highway speeds. If the maximum blade speeds are halved, and the maximum drawing speeds are doubled, the cutting angle shown in Burton’s diagram is still off by a factor of four. In a real cut, which doesn’t sacrifice blade speed just to illustrate the magical powers of a draw cut, the actual angle would be no more than 10 degrees or so. Take the angles from his figure 117, and move them onto the blade, and you have something closer to the truth. The slight difference in the resulting slopes of the cutting angles can’t be illustrated, since the pixels would overlap. It would amount to a 29-degree angle versus a 30-degree angle, but even this would rely on a four-fold exaggeration in axial versus radial speeds. In short, the blade thinning aspect of draw cut theory was made from whole cloth, and people have apparently believed it ever since.
There are some interesting things going on when slicing, part of which is the sawing or dragging action of a blade, which primarily benefits cuts against soft and sticky targets that have strands of connective tissue, like meats. Draw cuts aren’t quite so effective against things like wood or metal, where the stiffness of the material maintains firm resistance against the sides of the blade, instead of just the edge. Against any metal armor, a draw cut will work only by abrasion, and we don’t cut metal by using knives for reciprocating saw blades, because it would take hours to make a cut. This might be why period illustrations of the inside fight show stabbing and wrestling, instead of people trying to merely rub sword edges against their opponents.
Similar to some of the mistaken ideas about the draw cut are some of the thoughts on the increase in the cutting power of a slightly curved blade. Real cuts are made against extremely curved shapes, like arms and heads, and what initially matters is relative curvature. The slight difference between a section of a straight and a curved blade is overshadowed by the curve of the target. Though certainly the curved blade would be preferable in fights against square-sided people, I don't think it matters much against round people. Once the edge has penetrated through armor and skin, the muscle should be cut quite well by either type of blade. A quick bit of testing should let us closely quantify the effects of blade curvature on high-speed impacts.
The modern thoughts on this might also stem from Burton's work. He thought that
somehow all the momentum of the blow gets concentrated at the bend in the blade,
which is a really strange notion. It makes me imagine a particle called a forcetron,
which moves around in steel, traveling up and down the blade, looking for likely
impact locations. Instead of ferrite or martensite, we get a blade made of momentumite,
which exists only in curved blades, thus explaining their incredible momentum.
Of course, you could explain the complex patterns of blade vibrations by alluding
to the forcetrons, which run around and high-five each other at their post-impact
victory parties. Just remember that the 19th century arguments between the benefits
of straight versus curved sabers (especially in regard to mounted combat) never
got settled, which implies that neither side ever produced clear evidence of
superior cutting.
There
are innumerable problems with the modern theories of sword dynamics, and the
worst is that we don't even have a good theory. We pretend we do, and allude
to all sorts of mysterious complexities that are inherent in sword impacts.
However, upon further digging, it becomes obvious that people have wildly differing
ideas regarding how a sword works, even at a very fundamental level. People
in non-Western countries probably assume that given our technological mastery,
we must be absolute masters of sword physics, but in truth we just have some
odd and convoluted notions that don't actually explain anything. Our ideas aren't
used to make predictions or conduct experiments, and don't in any way address
impact behavior, but are simply invoked to explain away issues of rotational
dynamics and impact behaviors that aren't even vaguely understood.
I don't yet know where many of our modern notions come from, but it certainly
doesn't seem to come from Renaissance studies of sword dynamics. All we know
is to strike with the percussion point, which is always about a third the weapon's
length back from the tip, just as fencing masters and cavalry manuals tell us.
We obsess over the location of the percussion point, and the web is full of
deep discussions about it, including charts of observed percussion point locations.
You can find out anything about the percussion point that you could possibly
want to know, except for a few piddling details, which are completely wrong.
These exceptions are; what it is, where it is, why it's important, and why we
even care.
The percussion point of a sword is just the same as the impact points and pivot points that I’ve been discussing. The phrase “center of percussion” is a scientific term that predates Newtonian mechanics, and referred to these rotational motions in the 1600s, 1700s, and 1800s. The term is still used this way in physics, and most other fields besides modern sword physics, a term which is probably something of an oxymoron. Some modern swordsmen obsess over the location of the percussion point because they’ve been told that it’s extremely important, and that every swordsman must know its location. Historical swordsmen concerned themselves with it because it truly was important, for all the reasons put forth in this article about pivot points. The fundamental reason that physicists and swordsmen have different meanings for the term percussion point is perhaps that quite a long time ago real swordsmen switched to guns and forgot all about swords, while physicists preserved the original meaning and importance of the word.
The reason physicists know about the percussion point is that they used to carry swords on their hips, back when common English included the words percuss, percussed, percussing, percutient, percussent, percussion, and repercussion. Some of these words still survive, but mainly because physics and dynamics preserved them as scientific terms, divorced from common use. Repercussion is the only oddity among these, since its scientific meaning is lost and we only know that it refers to unintended consequences, or a backlash. Scientifically, it apparently once described what happens when you make a strong blow at a resilient body, which results in an elastic collision that preserves your blade velocity, but reverses its direction. This is extremely hazardous, so when you’re test cutting, you need to beware of the possible repercussions, since they could cut off your leg.
The word percussion just means impact, so the phrase percussion point literally translates to impact point, and center of percussion is just the center of impact, terms that I’ve used throughout this article. In modern physics, the words are synonymous, for the same reasons that I was sometimes using the phrase impact point, and sometimes using the term center of impact relative to the ____. The points are mathematically the same, yet also physically opposite. In discussing the mechanics of a sword, or any other solid body, the choice of terms is rather arbitrary.
Additionally, early physicists were also well versed in music, as shown by some of their ingenious musical experiments. There’s no way that they could mistakenly refer to the sword’s equivalent of the node on a vibrating string as the center of percussion, or the percussion point. If they wanted to talk about the node of oscillations, they’d have done so with the correct scientific terminology. Or more properly, science would’ve preserved whatever term they used to describe it, and we’d be using similar phrases to describe both the node of oscillation on a vibrating string, and the optimal striking point of a sword. We don’t have such a confusion, simply because our terminology comes from sword wielding physicists who had absolutely no confusion about these two very different concepts. In the 1600s a very famous and difficult problem was to analytically find the percussion point of a sword. They took this to of course be the same problem as finding the center of oscillation of a pendulum.
The term center of percussion has over the years picked up many other meanings, sometimes referring to a fixed point on the blade, sometimes to the optimal impact point for a particular situation. An example of this would be referring to the center of percussion as the percussion point relative to the instantaneous center of rotation, which in fact is the point on the blade that can dissipate the maximum energy, although not necessarily make the best cut. In a non-rotating blade, which is simply moving linearly, this point is at the center of mass, which is something they knew at least by the early 1700s, if not long before. Center of percussion also came to mean the ideal striking point, the point that produces the least hand shock, and finally the node of oscillation that appears when you slap your blade. So when you strike, you won’t miss the center of percussion by very much, since it has so many different meanings that you can’t avoid hitting near somebody’s definition of it.
As
to why we’re still obsessing over the percussion point, given that we haven’t
known what it is in quite some time, I must admit ignorance. Once we’d decided
that it was the node of oscillation, about a third back from the tip, a location
that can’t vary much, why continue to search for it on each and every sword?
I assume that earlier authors had somehow conveyed the importance of finding
its location, without clearly explaining what it was. Sir Richard Burton did
say that every swordsman must know the location of his percussion point, but
was a bit vague about how to go about it. He did say that to find it the cavalrymen
go into the woods and hack at limbs, looking for the impact point that gives
the least hand shock. But most notably, he never said that you can just slap
the slide of your blade to find the percussion point. Since he talked about
swords to just about everyone, and apparently no one told him about the blade
slap, I assume that no one in that era thought that the percussion point could
be found by slapping the blade. But he did tell of an ingenious technique for
finding the percussion point, in use at the Tower of London, which involved
swinging the sword like a pendulum and timing its oscillations.
More insight can be gained by a close examination of what Sir Richard Burton actually says about the center of percussion in footnote 10 of his 1876, A New System of Sword Exercise for Infantry:
In the Regulation sword the "centre of percussion" is about one-third from the point; here there is no vibration, and consequently the Cut exercises its whole force. The "centre of gravity" is in the third nearest the hilt, and the "balance" of the sword results from the relative positions of the two centres. In light swords these points may be farther apart than in heavy blades; they should be closer in straight than in curved swords, and nearer in thrusting than in cutting weapons.
Note that he says the “balance” of the sword results from the relative positions of the two centers. There is no physical way that the location of the node of vibration of the blade can affect the “balance “ of a sword. The “balance” is purely determined by the dynamics, which is the interplay between the balance point, center of percussion, moment of inertia, and mass. However, he’s also a bit confused, as he is about most things, by the vibrations. In a regulation sword, both the center of percussion and the node of oscillation are very close together, just like a baseball bat. Note that he mentions how close the two centers are, as you pull them together, you start to make my little rectangles into squares. Again, at the end of chapter 2 from his 1876, New Sword Exercise for Infantry, we have the following comment, where he doesn’t talk about vibration, but a jar to the arm that occurs when you don’t cut with the true center of percussion.
The Cuts must, as a rule, be delivered within eight inches of the point and at the "centre of percussion," so that the sword may clear itself and the arm escape a "jar."
Burton makes this comment about sabers:
However well made and scientifically poised be the blade, it is subject to several variations of equilibrium according to the position in which it is held. The nearer the centre of gravity approaches the hilt, the lighter and the better balanced will be the weapon, and vice versâ. Therefore: "It should be our principal object to effect this improvement without changing the proper centre of percussion and the other requisites for offence and defence.
Here he implies that as you move the center of gravity back, you can change the location of the proper center of percussion. Moving the center of gravity back has almost no noticeable affect on the location of the node of vibration. Obviously he had a clue about what was going on, but not a really clear idea. If he'd really understood it, he'd have written it down for us, and we'd never have gotten into the mess we're in now. But during his era, apparently some people still knew at least a bit of the knowledge. This makes me wonder whether the last person who really knew what a pommel was for, and how to adjust the center of percussion, quit working with swords and retired, did they know they were the last living person that could clearly explain a sword, and did they turn the lights off before they left?
Another revelation comes from just getting the feel of authentic swords. ARMA Director John Clements has been quite insistent that reproduction swords don’t handle like authentic ones, and although he has received tremendous criticism from some quarters for this position, he his quite correct. And has been backed up in his view by collectors, curators, more than a few fellow leading practioners, and by master swordsmiths. Unlike most all of today's reproductions, where the percussion point’s location is almost random, tight control of the pivot point location makes authentic swords behave in very logical and predictable ways. When we pick up an authentic sword, we feel its weight and the torque required to hold it horizontally, which is called the static moment. If the percussion point relative to the cross is at the tip, then the swords moment of inertia about the cross, which is a fair measure of how hard it is to maneuver the sword, is just the static moment times the blade length. The way the sword will naturally rotate during a swing is just a function of the square root of the blade length, and the tip inertia is just a function of the mass times the balance point to blade length ratio, which is just the static moment divided by the blade length.
All this means that when you pick up an authentic sword, you’ve already measured all of the relevant rotational dynamics. With reproductions, as currently made, you can’t be sure of anything. You have to pick it up to see if you like the static feel. But since the pommel is used to “balance” the blade, just as we’ve all been taught, the static feel might be unrelated to the rotational inertia, so you have to swing it around till you get a feel for it. And since the percussion point could be just about anywhere between one half the blade length and infinity, the impact behavior is likewise almost unpredictable. However, the bright side to all this is that after a hundred or more years of ignorance, we now can easily make extremely good reproduction swords, since we still have good blade smiths [it just ain't cheap, and it takes time and skill]. What we’ve been lacking is the trick of sizing a pommel by swinging the sword like a pendulum. The results of this test will immediately show up in the finished swords, some of which will then feel horrible. If the pommel exposes underlying blade heaviness, then the only solution is to shave mass from the blade, and then resizing the pommel, since blindly increasing the mass of the pommel is not an option on a real sword.
Some Original Sources
Before
anyone runs off screaming that no one could’ve known this back then, let
me offer a small bit of evidence that they at least knew some of it, if not
more. I tracked down references to percussion, now a rather obscure term taking
up at most a few lines in a physics book. The bulk of the work on it appeared
to occur in the 1600s. Galileo wrote a track called “On the Force of Percussion”.
It’s usually bundled with his book “Two New Sciences”, which
is fascinating in its own right, not to mention the bits on the physics of lancing,
wounding, striking, and deflecting. But mostly it concerns impacts, and he said
he burned thousands of hours thinking about it. Interestingly, he did this work
at the Venetian Arsenal, where he worked on impacts and pendular motion, not
to mention the parabolic flight of cannon balls. He even came up with new methods
for the workmen in the shop to produce more accurate parabolic sections for
structural applications. But from what he wrote, it seems he spent much of his
time hanging out with soldiers and students, discussing impacts. For those who
think that swords were designed by nothing but feel and artistic sensibilities,
you might wonder what kind of people the Venetian Arsenal’s “human
resources” department was looking for when they hired Galileo. I don’t
think they were after his aesthetic sensibilities, and he certainly wasn’t
hired to make tea.
Galileo
corresponded with Marin Mersenne (left), in Paris, who served as the clearinghouse
for all the scientific correspondence occurring in the early 1600s, corresponding
with Fermat, Rene Descartes, and countless others. When he died, he still held
letters from 70 different scientists, most of them famous to this day. Some
of the best investigations into impacts and pendular motions were carried out
by Christiaan Huygens, who was communicating his results to John Wallis, one
of the founders of the Royal Society, and Isaac Newton, among others. Huygens
opens his work “The Pendulum Clock” with the following paragraph,
as translated by Professor Michael S. Mahoney, chair of the Science History
Department of Princeton University.
Some time ago, when I was still a boy, the most learned Mersenne proposed to me and to many others the investigation of centers of oscillation or agitation, a very famous problem among mathematicians of that time, as far as I can gather from the letters he sent me and from the recently edited letters of Descartes containing his response to Mersenne on these matters. Mersenne proposed further that I should find these centers for sectors of circles, hung both from the vertex and from the middle of the arc, and moved from side to side, as well as for segments of circles and for triangles hung first from the vertex and then from the midpoint of the base. The problem comes down to finding a simple pendulum, i.e. a weight hung on a string, of such a length that it makes oscillations of the same time as those aforesaid suspended figures. At the same time, indeed, he promised me a rather large and coveted reward for my labors, if perchance I should solve the questions. But no one at that time obtained what he desired. And, as for me, since I found nothing that made clear even a first approach to this contemplation, repulsed from the start, I abstained then from a lengthier investigation. Indeed, those distinguished men who hoped to accomplish the thing, Descartes, Honoré Fabri, and others, in no way hit the mark, except in some few simpler cases, and even of the latter, it seems to me, they adduced no proper demonstration. This will, I hope, be manifest by comparison with the things I set forth here, if perchance someone should compare what has been set forth by them with our material, which I judge to be demonstrated by more certain principles and which I have found to agree precisely with experiments.
Well, I noticed that the original problem seems to be to find the center of percussion for sectors of circles or triangles, held from the big end or from the point. I’d had to solve the same problem to come up with the formulas for correct pommel mass, so I e-mailed Dr. Mahoney, explaining my research, and inquiring whether he knew who was putting up the reward, suggesting that it might be a military arsenal. He went through their personal correspondence, and replied that the reward that Mersenne mentions was simply one of becoming the most famous and renowned scientist in Europe, but that the problem was indeed originally one of finding the percussion point of a sword. What’s interesting is that Huygens says, “The problem comes down to finding a simple pendulum” so the connection between the center of percussion and pendular motion was already well established. If you hold to the view that Galileo invented the pendulum, it would be unlikely that someone in the brief span of time between the work of Galileo and Huygens would’ve stumbled across the relation between the period of a pendulum and the percussion point of a sword. Especially since this same connection eluded all the 20th century sword researchers, though many of the 20th century researchers were distracted by fantasy sword physics. As the investigations into pendulum testing go back past Galileo’s era, I would point out that there are many reasons to doubt that Galileo invented the pendulum, including his father’s pendulum research as reported by Stillman Drake, his lack of claiming any credit for it in his book “Two New Sciences”, where he introduces it as a “very dry subject”, and Leonardo DaVinci’s 1474 sketch of what looks like a pendulum clock, though I’ve not seen this drawing, so for all I know it could be a sketch of an automatic pommel sizer, given all his other innovative work on weaponry.
In this work, Huygens also mentions the following:
But it is not our intention to pursue how one finds the centers of gravity of wedges on plane figures; they are already known for many wedges. For example, if figure BAD is a circle, DH will be equal to 5/8 of the diameter. If it is a rectangle, DH = 2/3 of the diameter. Whence also the reason is clear why a rod, or a line endowed with weight, suspended from either end, is isochronous with a pendulum of subsesquialterate length; that is, by a consideration of the line just as if it were a rectangle of minimum width.
If the figure is a triangle with the vertex upward, DH is 3/4 of the diameter. If the vertex hangs downward, DH is 1/2 the diameter.
The
first line accidentally referred to the center of percussion, or center of agitation,
as the center of gravity, since the center of gravity of a circle is in the
middle, of course. The last line gives the percussion points for a triangle.
From the hilt, a bare blade with a triangular mass distribution pivots in the
middle. Held from the tip, it indeed pivots around a point ¾ of the length
from the tip. However, he starts by saying that these points were already known
for many wedges, and then rattles off some locations. Obviously finding the
actual answer about the triangle isn’t the original problem, since here
he says it was already known, and since the pendular connection was already
known, they could’ve just sawed out a triangle and tested it. The problem
he’s dealing with is one of uncovering the fundamental reasons for this
type of rotational motion, based on all the little bits of mass that make up
the object. But this isn’t exactly walking around knowledge, except for
the all important sword connection. So it would be very hard to argue that they
didn’t know about percussion points, when quite obviously they did, and
discussed it in a sword problem, in a world where scientists carried swords
around. One of these scientists was Rene Descartes, who definitely worked on
the sword problem, and was a soldier who all his life wouldn’t go anywhere
without his sword and a purple feather in his hat. (He also advised that unless
you sleep late as possible, you’ll not think clearly, so he was surely
on to something).
We’ll continue to investigate the connections in historical sources, which shouldn’t be nearly as difficult to round up as historical fighting manuals, since these documents would be discussing the physics of impact and pendular motion. A view commonly held among historians of science is that the major advances in physics in the hundred years prior to Newton’s “Principia” were the result of investigations into impacts and pendular motion. Since the sword community has been out to lunch, we’ve not known that impacts and pendular motion are the heart and soul of sword physics, or that European swords were carefully set up to be pendulums. Although there are few subjects as boring as pendular motion, there are few as interesting as sword dynamics. The scientists back then obviously knew the connection, so maybe they were also possessed by the same sword demons that afflict us all. We can also go through the museum samples, and see how tightly the percussion points are being controlled on the surviving swords. We can especially see if there is some time window prior to which the percussion points locations get sloppy, as if they were waggle testing instead of pendulum testing, or even failing to control the percussion point at all, except by coincidental feel, just like the later reproduction swords.
We basically have a large list of suspects, including almost everyone who corresponded
with Mersenne, since he was apparently talking up the sword problem amongst
all the scientists. Many of these wrote books on local mechanics, some with
titles like “Free Impacts” and illustrations that look like a hand
holding a sword, and others that discuss the author's “Doctrine of Percussion”.
So maybe there are surviving texts that will tell us not only how they thought
a sword works, but also possibly how a sword does in fact work. Just because
it’s pre-Newtonian, doesn’t necessarily mean it was wrong. On top
of this we might find personal letters where someone spills all they know, so
maybe we can make some progress on answering the question “What did they
know, and when did they know it?”
The
reproduction swords being made today vary widely in percussion point location
and moment of inertia, so that practitioners have trouble communicating. Although
they may for example all look like longswords, their handling properties vary
widely. Remember that we're all still coming out of the era of the 20-pound
war sword. We're getting much closer to historical accuracy, but there are still
a great many swords out there that don't behave quite right. If a particular
passage from a historical fighting text instructs to oppose a cut with a thrust,
but the reproduction sword we use has a moment of inertia that's twice the historical
value, which is not uncommon, then the technique will only work when the timing
and geometry have been sufficiently altered to handicap the thruster and favor
the cutter. The practitioners might become skilled at using altered techniques,
until one of them buys a more accurate sword, and then they're back to square
one. The technique they trained in doesn't quite work anymore, and they're discouraged
by their lack of progress. Many end up developing a technique to match the first
swords that they purchase, and then keep buying similar swords that work with
their techniques. It ends up being a vicious and discouraging circle. As Clements
has said, if the tool you use is a distortion of the real thing, your understanding
of fighting is affected, your techniques are off, and all of your interpretation
of the source manuals is distorted too.
Having a sword with a high moment of inertia is bad, but then trying to invent a style that uses it for close-in draw cuts makes things much worse. The results of this are quite obvious when swordsman try to interpret period drawings and their descriptions of long-range, high-velocity, full-strength cuts. These get turned into short stepped, slow, close-range draw-cuts impacting a third back from the tip, at the assumed location of the center of percussion. The cut is slowed down to maximize the drawing action, which interferes with footwork, the delivery, and the follow through. One indication that this can't be right is that slow swings don't work with the period methods that utilize counter-strikes. As long as both practitioners move at half speed, the blades meet up correctly. But a person thinking "slow but with power" will be a late as soon as his attacker switches to full speed. Techniques that depend on relatively equal blade speeds can't exist at anything other than full speed, otherwise the winner would always be the person who "cheated". The whole basis of a real combat art is that everyone already is cheating, in every conceivable way. With masters working to invent new techniques and secret methods, an important fighting trick like "swing it faster" wouldn't stay secret for long. Strength and speed can confer an unfair advantage, so use them. Everyone can have good half-speed form, and think their cuts are powerful, but maybe there's a reason why successful warriors were described as strong, powerful, or swift. The masters all used a variety of methods at the sword, and full speed was one of them.
The only caveat about full speed cuts is that as soon as you miss, your blade is still traveling at high speed, but instead of approaching the target, it's heading the wrong way. So if you've swung with all your strength in getting the blade up to speed, you'll have to use all your strength again, to kill off its velocity, unless you bring it back around for another attack, using a circular motion. It will take you just about as long, both in time and distance, to kill the blade's velocity as it did to speed it along in the first place. So you'll naturally end up in one of the other guard positions. Slow speed techniques wouldn't require cuts to always move from guard to guard, since you could just stop or even back up. The other part of this is what happens when you do hit the target. If you're using slow speed impacts at the node of oscillation, you've actually hit far behind the true center of percussion, and the hilt makes a rapid drop in velocity. Essentially, not only do you get hand shock, this hand shock is in large measure stopping the hilt. So hitting and missing leave you in very different positions. If you instead make strikes nearer the tip, and nearer the true center of percussion, hits don't significantly affect the hilt velocity. As shown in the section about pivot points, hitting the target basically just adds a new rotation to the hilt, instead of trying to stop it. So your hands will follow the same path whether you hit the target or not. If you're making full speed swings, you'll naturally recover to the next guard position whether you hit the target or not. This moves you to a style of swordsmanship that can use sequences of complex attack patterns, as we find in mnemonic poems. Of course, the opponent will be trying to break up the attack sequence, because opponents won't just play along, as is their nature. We all know to strike with the percussion point. Well, it's not at the node of oscillation. It's the actual percussion point, and relative to the cross, it's much closer to the tip.
The other result of invalid cutting theory is the common misconceptions about the physics of cutting, which result in styles of cutting that just won't work. Some practitioners maintain that they swing slowly, yet by moving correctly and putting their body weight into the blow, still achieve a powerful cut. In truth the correct biomechanics maximizes the sword's impact velocity in a given situation, and anything less is just a slow motion illustration. The body's weight can be used to accelerate the sword prior to impact, but it doesn't ride along with the blade. You might think that a good cut results from a combination of speed and form, so try a simple experiment to isolate the relative influence of each. First, try and cut into a tree with nothing but high blade velocity, by holding the sword out the window of a speeding car. Compare this to a cut on a tree that uses no blade velocity, but correct form, by laying the blade against the tree and changing your pose till a chip flies out. The form is simply there to get the blade up to high speeds while maintaining proper edge alignment, with some tactical considerations thrown in. You might argue that you're putting tremendous torque on the weapon, adding power to the cut. But for example, a 60 mph (27 m/sec) tip impact with a typical single-handed sword, which stops in 3 inches (76mm), will have an average impact force somewhere around 150 lbs (670 N). Your maximum static wrist torque would add less than 5 lbs to this value, or about 3%, so you might as well ignore it. When Tiger Woods swings with all his form, but at only half speed, the ball won't go as far. The distance comes from the speed of his club-head, and his form gets the club head up to speed. Cutting slowly, but thinking that your putting all your body behind the cut, is no more effective than trying to cut through the target by wishing really, really hard, unless you're applying tremendous torque to the blade.
The only way to objectively measure your cutting power is to observe the effects on your target. We’ve been trained to know what a powerful cut feels like, but the problem is that we’ve been trained to strike a third back from the tip, at the node of oscillation, regardless of the true location of the sword’s center of percussion. With a medieval sword, cuts at the node of oscillation will produce quite a tremendous hand shock. We’ve probably been thinking that this hand shock represents the cutting power. Especially since we were also thinking that hand shock is just blade vibrations. Many have commented that cuts with the tip feel weak, and thus are weak, and that’s the whole point of it. Cuts around the true center of percussion not only feel weak, they probably won’t be felt at all! This means you can’t judge the power of your impacts by feel. Some might soon be tempted to think that if they didn’t feel any shock, the cut must’ve been powerful, but this too is wrong. If you hit with the center of percussion, you wouldn’t feel anything no matter what the impact velocity was. It all comes down not only to how much energy was delivered into the target, but really how much damage was done. The energy is measure in Joules, and I suppose the damage could be measured on a case-by-case basis. But this is certainly different from the subjective self-reporting of cutting power, like “My last cut was [somewhat|very|incredibly] powerful”, which doesn’t have any measurable units. Instead of hard measures like inches of penetration in a particular material, it sounds more like people trying to describe how beautiful the cut felt, using the mental equivalent of “units of beauty”. Just beware that the resistance offered by the target material is a dominant factor in the outcome of the impact, something that Galileo said, “everyone knows”. So make sure your chosen target materials won’t lead you to optimize toward an axe or a foil.
As evidence that our everyday understanding of impacts and motions is greatly inferior to that of people in the Renaissance, I offer this tidbit from Galileo, "Two New Sciences" - translated by Stillman Drake pg. 241-242, based on an earlier edition by Antonio Favaro, (Florence, 1898) "Opere di Galileo Galilei", volume VIII, pg. 291-292:
To that which has been said up to this point about these impetuses, blows, or let us say impacts of projectiles, we should add one other very necessary consideration. This is that it is not sufficient to have in mind just the speed of the projectile, in order to determine fully the force and energy of its impact, but it is further necessary to specify separately the state and condition of that which receives the impact, in the effectiveness of which this [condition] has a great share and contribution in several respects. First, everyone understands that the thing struck suffers violence thereby from the speed of the thing striking [only] to the extent that it opposes this and entirely or partly restrains [frena] its motion. For if a blow arrives on that which yields to the speed of the striker without any resistance at all, there will be no blow. And he who runs to strike an enemy with his lance, if it happens that as he overtakes him the enemy moves in flight with like speed, will effect no blow, and the action will be a simple touching without wounding. If an impact is received in an object that does not yield to the striker entirely, but only partly, the impact will [do] damage, not with all its impetus, but only with the excess speed of the striker over the speed of retirement and yielding of the thing struck. For example, if the striker arrives with ten degrees of speed upon the thing struck, which, by yielding partly, retires with four degrees, then the impetus and impact will be as of six degrees. And finally, the impact on the part of the striker will be entire and maximal when the struck does not yield at all, but entirely opposes itself and stops all the motion of the striker, if indeed this can happen.
I said [impact] "on the part of the striker," because if the struck moves with contrary motion against the striker, the blow and encounter will be made so much the more strongly, as the two contrary speeds united are greater than that of the striker alone. Moreover, it must also be noticed that to yield more, or less, may derive not only from the quality of the materials, harder or less hard, as of iron, or lead, or wool, etc., but also from the placement of the body that receives the impact. If this placement is such that the motion of the striker comes against it at right angles, the impetus of the impact will be maximal; but if the motion comes obliquely, and gives a slanting blow as we say, the blow will be weaker, and the more so according to the greater obliquity. For any object obliquely situated, though of very solid material, does not remove and stop all the impetus and motion of the striker, which escapes and passes on beyond, continuing (at least in part) to be moved over the surface of the opposed resistant.
Galileo wrote this passage to show that the impact of a cannon ball is maximal when the target surface is perpendicular to the projectile's trajectory at impact, not necessarily when the target is either vertical or horizontal. But to explain his reasoning he ties it to some impact physics that everyone already understands. His passage indicates that everyone in his day understood the essential concepts of closing velocity and target resistance. He's also putting actual numbers on these closing velocities, so in the 400 years since his day, we've gone backwards in our sophistication and knowledge about sword combat. Instead of saying, "the impetus and impact will be as of six degrees", we've been reduced to saying "My blows feel powerful!" This passage also implies that if you want to maximize the strength of your opponent's blows, use direct opposition, or at least static parries. For those of us who would prefer not to convert our opponent's swings into hard blows, unless absolutely required, maybe voiding or deflection would be better, since it's only the target that converts a swing into a blow. If you aim for audience entertainment and thus want to maximize the number of powerful blows, then stay with edge-on-edge sword banging. But this passage implies that everyone back then would think it was a very counterproductive way to fight. And if they thought that maximizing the closing velocity maximizes the impact, as this passage implies, then they'd undoubtedly conclude that they should swing hard, and hit with the fastest part of the blade, near the true percussion point, up near the tip, where the blade is especially sharp.
Once the cuts are slowed down, the entire range of possible maneuvers actually expands, because blade velocity and momentum are no longer dominant factors in maneuver dynamics. Once this happens, understanding the historical source manuals becomes more a problem in trying to turn a system based on the outcomes of real physics into a sword ballet based on fantasy sword physics. You end up facing the vast array of possibilities present at slow speeds, cherry picking options that kind of, sort of, look like something done in one of the manuals. This may be why many attempts to extend sport-fencing techniques over to real cutting swords have failed. Fencers don’t take real swings, just simple wrist cuts, and with heavy swords these can’t get the blade velocity very high. If it did, they’d be breaking at least a few bones. The openings that show up in high-velocity maneuvers, and the openings revealed in low-velocity maneuvers, are not the same -- in both striking and counter-striking displacements (i.e., parries). If the high-velocity cuts are transformed into slow draw-cuts, what we’ll get is yet another fencer’s parody of the earlier swordplay, but with the incorrect techniques executed in German, instead of French.
We’re
still haunted by the idea that Medieval and Renaissance swordsmen were primitive.
We’ve since learned that their combat methods were very sophisticated, but are
still clinging to the notion that they couldn’t have been applying sound engineering
principles to their swords, but must’ve just been building them by feel and
an adherence to concepts of aesthetic balance. However, you don’t need to understand
all sorts of complex physics to get insight into how a sword works. I’ve just
explained rotational impact dynamics with nothing but a circle, a rectangle,
and a lever, so it might not be wise to assume that a people obsessed with the
geometry of sword combat didn’t do similar calculations. The insights shown
in many Renaissance writings on statics and dynamics point to this, especially
since the surest route to fortune has traditionally rested on developing better
methods for Europeans to kill each other. Many have the image of the crude,
barbarian, sword- wielding knights, and don’t stop to consider that some
of the knights would also be the rich elite who went to college and studied
Greek, Latin, and Mathematics. They’d also have a keen interest in understanding
the science of local motions, pendular motions, and impacts, which might be
at least part of the reason that the aristocracy was sponsoring a great deal
of the research in this field.
The center of percussion has nothing to do with blade vibrations, and on earlier cutting swords, as opposed to later sabers-style weapons, is probably found at the tip, the very spot the master Fillipo Vadi writing in the 1480s tells us to keep especially sharp for cutting. The pommel sets the location of this point, and isn't used just to "balance" the blade. The result of "balancing" by any of us, based on our wide experience and varied opinions, has resulted in objects that look like swords, but don't always behave like swords. To find the correct pommel size, hang the sword by the cross and swing it like a pendulum. Add mass to the pommel until it swings in time with a pendulum hanging even with the sword's point.
The rigid-body impact model best describes sword cuts. The sword community has lacked this model for a very long time, which has led to both some inaccurate reproduction swords, and improbable sword techniques that rely on physically impossible outcomes. These invented techniques aren't based on any historical or physical reality, but are mostly extrapolated from later fencing techniques, which can't be easily extended to long cutting swords, since modern fencing styles don't utilize high velocity, high energy cuts.
All of our existing reproduction blades need to be checked, and if necessary modified to bring them into line with the performance and behavior of authentic swords. Otherwise, we'll be misled about maneuvering speeds and impact dynamics, and we'll at best become masters of reproduction swordsmanship. Basically, we can change pommels, add extra weight to them, or grind them down. If the result is a sword that lacks authentic "balance", due to the blade design, it presents the perfect excuse to buy some grinding and polishing equipment, to recover the investment in our reproduction swords.
We certainly need to take many more measurements from authentic museum pieces
so we can produce accurate reproductions swords that have the same dynamics
as the originals, especially cross-sectional differentials, including the tangs.
The mass, moment of inertia, percussion point, and balance point are all related
by one equation. It is physically impossible to just get one of these parameters
wrong, so a reproduction either has them all correct, or has two or more of
them wrong. To date, we've just been looking at the mass and balance point,
while the moment of inertia and percussion point have been left with random
variations. This needs to be addressed.
"That there are persons of mistaken ideas in
almost every Art or Science,
is what few will deny. Yet I am inclined to believe there are more
erroneous opinions entertained with regard to the
Art of using the Sword than on most other subjects."
- Joseph Roland, The Amateur of Fencing, 1809
The author, George Turner, can be reached at:
Gturner6ppc@yahoo.com
Author's comments: Over the past century, a great deal of time has been spent wading through sword voodoo, trying to unlock the secrets and reveal the hidden mysteries, plus selling a thing or two. We’ve got legions of blade slapping morons around, all trying to top each other at unlocking the hidden secrets of “powerful” sword cuts. Now at last the scavenger hunt for the percussion point of a sword is over, and I must reveal that the elephant was hiding in the kitchen the whole time, in any physics dictionary under the word “percussion”. Even if I prove mistaken about parts of this research, I don’t think we’ll ever again be as screwed up about all this as we were in the 20th century. As a side note, sometimes someone will suggest that maybe the moment of inertia plays a role in determining a sword's feel, but get outweighed by those who say that sword behavior is so complicated that a host of other factors would also have to be considered. All of this has left us with a very poor understanding of sword dynamics, and an avoidance of the harder questions. Combine this mere lack of understanding with the totally mistaken concepts of the center of percussion, hand shock, and cutting power, and we're left with modern debates where none of the arguments even makes any sense. [So when you read about Medieval philosophers thinking that if they just add a few more spheres to their model of the heavens, they’d get the model to agree with the observed planetary orbits, just remember the day when you thought, “If I add just a couple more nodes of vibration to the blade model, I think I’ll have this all figured out.”]. Too often I've noticed people discussing swords and not sounding at all similar to other enthusiasts of weapons, such as world-class gunsmiths or marksmen who are very technical. By contrast, the sword enthusiasts end up instead sounding like a couple of valley-girls debating the design attributes of an "awesome" handbag. What's our vocabulary for picking a modern reproduction sword? We go by the manufacturer, brand name, attractiveness, custom detailing, grip color, how "rare" and exclusive it is, and the price. Sound familiar? This is how we talk about new sneakers or a new dress, not a weapon. You might argue that swords come in a bewildering variety of shapes, and include all sorts of subtle details, which can't be described by simple measures. Yet firearms also come in a bewildering variety of shapes, but instead of throwing up our hands and ascribing the differences to unknowable mysteries or gun fashions, we actually bother to understand how they function. Some of our leading swordsmiths can build top quality weapons, but if we lack an understanding of why these weapons perform, we won't appreciate them, or the skills that they embody. In our current marketplace, often a pretty leaf spring with a pretty red grip outsells a better-crafted sword, even if the better sword is the culmination of immense time, labor, research, craftsmanship, and a good gut-level understanding of sword dynamics. Without the knowledge of dynamics, much of our debates boil down to whether a Gucci purse is worth the money. Discussion of the properties of historical swords should be, and can be, better than this.
See also: What Makes an Effective Sword Cut
and "Hey Mister...is that sword real?"
|
|
|||
|
|
|||
|
|||