
 |
||||||||
|
|
||||||||
Once you know that an impact will cause a rotation, some other interesting things come to light. Since the pivot point undergoes no change in motion, it could be attached to another body, such as your hand, without affecting the sword's motion in any way. And if your hand isn't affecting the motion of the sword, then by action and reaction, the sword is also not affecting the motion of the hand. You could even have the pivot point attached to a moving car, with a bearing, and there would be no forces on the bearing, other than the forces from having the blade spinning round and round like an unbalanced propeller after the actual impact. So if the bearing was attached at the natural pivot point of the impact, it would receive no impact forces, and thus it really wouldn't matter whether the bearing was real or imaginary. Either way, it would play no part in the resulting motions, since the sword would naturally pivot around the bearing anyway.
So let's have this imaginary bearing serve as the fulcrum for a lever. Since our fulcrum is just as imaginary as our bearing, its physical presence likewise doesn't matter, as it receives no forces from the impact. Since the impact is altering the motion of the sword, the sword resists, because of its weight. Just as heavy objects are harder to get moving than light objects, so heavy swords are harder to accelerate than light ones. But once in motion, heavy objects are likewise harder to stop. This resistance to changes in motion is what makes an impact work. Let's treat this resistance of the sword as something concentrated at its balance point, or center of mass, and recognize that we're now pushing on it with a lever. The force pushing on the lever comes only from the impact, and this force is of course applied only at the point of impact on the blade.
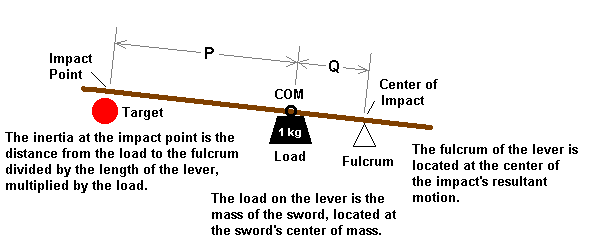
Figure 7 - The sword acting as a lever during impact.
So we have a point that doesn't undergo any change in its motion, which I could refer to as the pivot point, or the center of the impact's change in motion, and this point we treat as the fulcrum of an imaginary lever. The load on the lever is merely the mass of the sword, which we simply treat as being concentrated at the sword's balance point. The force on the lever is applied at the impact point, and this point on a lever is called the effort, since on a real lever that is where you apply your effort. The length of the lever arm is just the distance from the fulcrum to the effort, which is just the distance from the impact point to the pivot point. We call this a class-2 lever, since it has the load between the fulcrum and effort. The theory of this kind of lever was well described by Archimedes, so this is nothing new. The mechanical advantage of the lever is the ratio of the distance from the fulcrum to the load, to the overall length of the lever arm.
Normally, we think of a lever as multiplying the applied forces, but if we blindfolded someone and had them use a lever, they couldn't tell how much the load actually weighs, nor could they guess the lever's mechanical advantage. All they could tell you is how hard it is to move the lever by applying forces at the effort. From their standpoint, it makes just as much sense to talk about the mechanical advantage dividing the load, instead of multiplying the force. If the lever were acting horizontally, instead of vertically, the only way to measure the load would be by its resistance to acceleration, due to the mass. But since they still wouldn't know the mechanical advantage of the system, all they could say is how much the lever resists acceleration, as measured by pushing on the handle. Let's term this resistance to acceleration inertia, for lack of a better word, and say that it's the measure of both the size of the load, or mass of the sword, divided by the mechanical advantage of the lever that naturally forms from the free rotation of the sword, which occurs due to the impact.
Given that on authentic swords, at least as far as I have yet determined, the pivot point is at the cross, relative to an impact on the tip, finding the tip inertia is trivial. It's just the balance point to hilt distance, divided by the blade length, multiplied by the total weight of the sword. You can measure it with a scale and a pair of dividers.

Figure 8 - A sword as a lever during a free impact.
The tip inertias on authentic swords probably don't vary by much between types, as each sword was used to attack the same basic target. From person to person, swings are fairly similar in velocity profile, and swords would be optimized for the most common or most powerful swings, not the more obscure maneuvers. The behavior of the target determines the optimal combination of inertia and edge velocity in a cut at the impact point. Just as baseball bats aren't used to hit softballs, and vice-versa, each design having been adapted to the impact dynamics with a particular ball, the choice of tip inertia of a sword would be adapted to optimize the impact dynamics of strikes against the target. Since the people who are targets are physically similar, the requirements for optimal impact inertia likewise shouldn't vary much. However, trends in armor design may play a significant role in the historical selection of tip inertia. If forced to guess at a typical example of tip inertia, I'd go with something close to the mass of a baseball, or 5.12 ounces.
The inertia of the straight staff is always very easy to determine, since all untapered staffs are similar. The inertia at the tip of a staff is always one quarter of the staff's mass. The inertia at the point that's one third back from the tip is always three quarters of the mass, and if you use the point about 21% back from the tip, where the impact point and pivot point are equidistant from the balance point, the inertia is exactly one half the mass of the staff. In fact, if you have the impact point and pivot point equidistant from the balance point on any object, the inertia at the impact point is exactly one half of the mass of the object. This is because the impact naturally forms a lever with a two to one mechanical advantage, because the load is being positioned exactly in between the fulcrum and the effort. Once you understand pivot points and levers, some otherwise obscure behaviors make perfect sense.
The inertia derived from the lever model makes rigid-body impact calculations very simple. Anyone who's had a physics class has had to study the impacts of particles, which involves concepts like the conservation of momentum, elasticity of the collision, etc. If you treat the sword's inertia, as derived from the lever model, as the apparent mass of a particle, you can just apply high-school physics to the problem. The target doesn't know that it's being hit with a sword, and can only react as if struck with a particular amount of mass, traveling with the blade edge's velocity at the impact point. You might say that the target can't determine whether a large rotating sword or a small piece of flying shrapnel struck it. The amount of mass that the target reacts to is just the sword's inertia at the impact point, traveling with the given edge velocity.
In deciding on the sword's optimal impact location, we're really just choosing the location on the blade that gives the best combination of inertia and velocity, since both vary all the way down the blade. The edge velocity obviously goes up linearly as the impact approaches the tip, since at the instant of impact the blade is rotating around some unique point, called the instantaneous center of rotation, which for a baseball swing is usually 6 to 8 inches inside the knob, or pommel. Keep in mind that the target doesn't care how your swing looked an instant prior to impact, only at the instant of impact. You hit the target with the blade, not the long, convoluted history of your swing. So just treat the inertia as the apparent mass of a colliding particle, and the rest is easy.
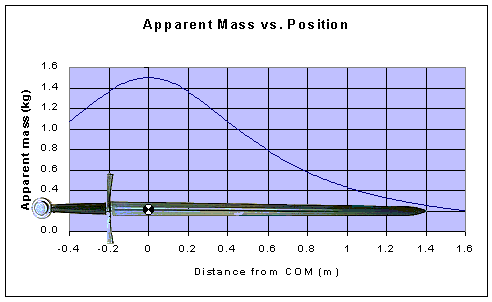
Figure 9 - A graph showing the inertia versus edge location.
Not to scale.
Figure 9 shows how the inertia of an object varies, and the basic shape of the curve is the same for all objects. As you vary the impact point to generate the curve of a weapon's inertia, it ends up being nothing more than the weapon's mass multiplied by the ratio of the pivot point's distance from the balance point, to half the perimeter of our rectangle, which is just the length of the moment arm of the lever. In the rigid body model, there are no magic spots, no clever tricks, just a smooth curve that describes the weapons inertia along the edge.
If you multiply the curve of the inertia by the edge velocity at each point you get the momentum, or quantity of motion, at each point along the edge. If I'd shown this line in figure 9, it would be a straight line, sloping upward from the instantaneous center of rotation, which is generally located a bit to the left of the pommel. The energy at each point along the edge is just one half of the inertia times the square of the edge velocity. The maximum energy along the edge is always found at the impact point that would have a relative pivot point coinciding with the instantaneous center of rotation. This makes quite a bit of sense, as this is the impact point that can bring both the linear and angular motion of the sword to a complete stop, and was known at least as early as 1721, when it appeared in Hutton's Mathematical Dictionary.
However, the point of maximum energy in a normal swing is quite far back on
the blade, often about one third from the hilt, and is certainly not normally
used as the striking point. The reason this point isn't used has to do with
collision dynamics. Against an extremely heavy target, hitting on this point
will completely stop the motion of the blade, but the impact velocity is very
low. It's more likely to bump the target, than to cut it. You'd only strike
with the point of maximum energy when you're using a sword to move heavy furniture,
and even then, expect some tremendous hand shock.
Using the inertia and velocity profile down the blade, it's easy to calculate
the effects of collisions with various targets, which takes into account the
elasticity and impact velocity. This may sound simplistic, but impact truly
is simple. All impacts have to obey the laws of physics, and there isn't any
magic going on in a collision, just physics. One of the first things you learn
is that a sword is not a very efficient tool. Most of the mass is near the hilt,
which remains in motion. Another thing you learn is that the collision's outcome
is dominated by the mass of the target. Heavy targets are best struck closer
to the hilt, light targets closer to the tip. This is because a light target
accelerates very easily, making it hard for the sword to build up cutting forces.
To counteract this tendency, you need all the edge speed you can get, and that
is maximum at the tip.
You'll also find that if you are approaching your target, as you would in a cavalry charge, the optimum damage is done much further back on the blade, whereas if you're striking at a retreating target, as with a backwards cut from a horse, the tip delivers the most damage. Likewise, if you have a very wide swing, which is largely linear motion, the optimal striking point moves a bit closer in, whereas with a wrist cut, in which rotation is dominant, the optimal point moves more toward the tip.
Also, you'll find that the elasticity of a collision goes down with the approach, or closing, velocity. A 2 mph crash just makes cars bounce off each other, being perfectly elastic. At higher speeds the collision becomes very inelastic, and you end up with one giant mass of twisted steel. All metal objects exhibit this behavior, and it tends to move the optimal impact point somewhat more toward the tip, where impact velocities are higher. In short, the determination of exactly the best point on a blade to strike with is heavily dependent on external factors, not necessarily related to the design of the blade. Each collision has to be considered on a case-by-case basis, but we can draw some generalities and say that for Medieval and Renaissance blades, strike near the tip, in what the German fencing masters called the weak (Schwech). If you've got a cavalry saber, strike about a third back from the tip, which is where you'll find the pivot point on a typical curved saber.
Striking with the pivot point, relative to your hand, so you receive the least hand shock, does not guarantee that the impact point was the optimal one for that situation. A common bit of wisdom is that strikes that deliver the least hand shock must inflict the maximum damage to the opponent, which I suppose comes from the notion that the sword has only so much "shock" in it, and if some of this is transferred to the hand, there must be less left for the target. Like almost every other bit of received wisdom about swords, this too is wrong. Impact forces cause the sword to change its motion, or yield to the blow, and the easier the sword does this, the lighter the blow. This is the fundamental reason that a very light sword can't deliver the same blow as a much heavier sword, which has more resistance to this change in motion. Hand shock occurs because in yielding, the sword encounters your hand as an obstacle that impedes this yielding. Slamming into your hand just urges the sword on. The improvement in the impact damage is very small, for single-handed swords doubtfully ever more than 2 percent of the blow, but the effect is always an improvement in impact damage, not a detriment.
Following are a few graphs showing how widely the impact behavior can vary due to target mass. Similar shifts in the optimal impact location also occur due to large changes in the ratio of linear to angular sword velocity. Much smaller shifts occurs due to variation of the elasticity of the collision with impact velocity. After the collision, the sword can retain linear motion of its center of mass, and can also retain angular velocity, which just means that either the sword still retains some of the original rotation, like a baseball bat after a hit, or that the tip stopped but the hilt kept moving, which is actually a reversal of the rotational direction, but the rotation still contains energy. In the graphs the light blue section represents kinetic energy that was present in the sword prior to impact, which can't be accounted for by any kinetic energy after the impact. This is the energy that was dissipated as heat, blunt trauma, material or tissue cutting, armor denting, or chipping the sword's edge. The only energy that can be spent in these ways is the energy that isn't still present in the simple motions of the system made up of the sword and target.
Don't worry over the exact numbers shown, since these graphs are given to illustrate a common behavior that all swords will possess. In the graphs, the hilt of the sword is to the left, and the tip to the right. The swords balance point, also called the center of mass, is at 0.0 along the x-axis.
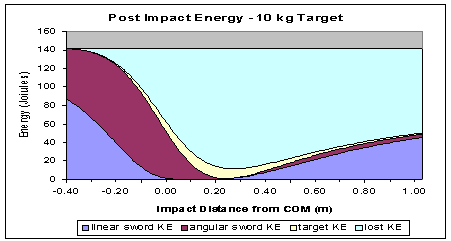
Figure 10 - An inelastic collision against a very heavy target.
The graph shows post impact energy versus impact point. The target kinetic energy
just propels the target. The lost KE is energy that was dissipated in the collision,
which is what inflicts the trauma. The initial kinetic energy in the sword was
140 Joules, which will run a 100 watt lightbulb for 1.4 seconds.
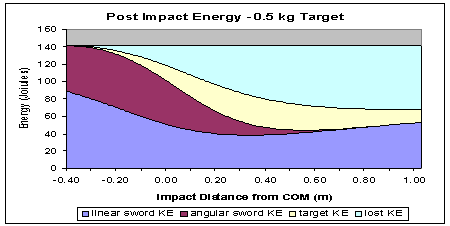
Figure 11 - An inelastic collision against a lighter target.
The light blue is the damage.
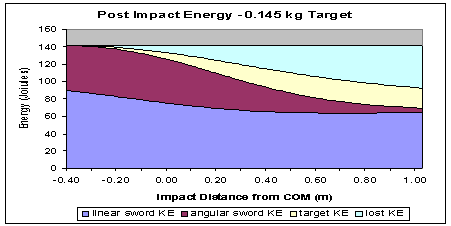
Figure 12 - An inelastic impact with a very light target.
The change in angular velocity of the sword is also easy to calculate. The linear impact model easily allows the calculation of the results of an impact, knowing only the initial velocities of both the target and the sword’s edge at the impact point, their respective inertias, and the elasticity of the collision. Since the initial velocity of the sword’s edge was a given, we can calculate the final velocity of the edge. Since the change in the motion of the sword is in the arc of a circle, centered at the impact’s pivot point, the change in angular velocity is just the change in velocity of the edge, divided by the distance from the impact point to the center of the impact. For a tip impact with an authentic sword, this is just the change in the tip velocity divided by the blade length.
You could perform the entire impact calculation using angular components. Just convert the linear impact forces into torques, by multiplying the impact force by the distance between the impact point and the pivot point, which is the length of the moment arm. This simple operation of multiplying a force times the length of a moment arm is why a torque is sometimes called a moment of force. The resistance to the impact force is still just the inertia at the impact point, but now having both the force and resistance acting around the fulcrum of the lever. However, resistance to rotation goes up with the square of the length of the lever arm, not linearly like a torque, so the resistance to angular acceleration is just the inertia at the impact point multiplied by the square of the moment arm of the lever, which we term the moment of inertia. The angular acceleration is just the applied torque divided by this moment of inertia.
Other ways you can approach this problem are to calculate the change in momentum at the impact point, which is just the inertia at the impact point multiplied by the change in velocity of the blade edge. This can then be taken to act on the center of mass of the sword, so you just divide the calculated change in momentum, termed the impulse, by the mass of the sword, and you get the change in velocity of the sword’s balance point. If you take the difference in the change in velocity of the impact point and balance point, and divide by the distance from the impact point to the balance point, you still get the change in angular velocity due to the impact. But this is a rather roundabout way of doing things.
The moment of inertia also measures how hard the sword maneuvers. Calculate the inertia at whatever impact point will make the sword pivot around the center of the handle. Multiply this inertia by the square of the distance between the impact point and the center of the handle, and you have the moment of inertia about the handle. You can also just draw another rectangle, almost identical to those drawn to find a pivot point, but with the base extending all the way from the impact point to the pivot point, instead of stopping at the balance point. The height is still just the distance from the balance point to the pivot point. The area of this rectangle, multiplied by the mass of the object, is also just the moment of inertia. From these rectangles, it’s trivial to derive such obscure things as the parallel axis theorem, which just says that as you move away from an objects center of mass, the moment of inertia increases according to the mass times the square of the distance from the object’s center of mass.
Aside from just moving the pivot point, the pommel also does some other interesting things. The pommel is very near your hand, so it doesn’t add much inertia about the center of the handle. It is on the inside of your swing, instead of near the tip, so you don’t have to accelerate it very much. However, when you make a strike near the sword’s tip, the change in the sword’s motion, pivoting near the cross, requires a significant increase in the velocity of the pommel. The impact forces are still acting through a lever, with a fulcrum located near the cross, but now with the pommel located on the other side of the fulcrum. If we leave the fulcrum’s location constant, then from the target’s perspective, the resistance to the resultant change in motion is the same whether we put the pommel eight inches behind the cross, or eight inches in front. The pommel on a straight cutting blade makes the sword hit harder, and by a very significant amount, while only making a small degradation in the sword’s maneuverability. So you’re getting the increased impact performance almost free. In short, the pommel is ingenious at many levels.
However, recall my earlier discussions on how objects rotate, and how adding a lump of mass at a particular point doesn’t change the pivot point relative to the mass. The pivot point relative to a pommel is always going to be about one fourth to one half back from the tip. If an impact occurs in this area, creating a change of motion centered on the pommel, then the pommel doesn’t get moved at all, just turned like a doorknob. This contributes next to nothing toward increasing the inertia, and thus the momentum, in the blow. For impacts about a third back from the tip, the pommel provides no benefit, and by slightly decreasing the sword’s overall maneuverability, is actually a detriment. However, as the impact point approaches the tip, the pommel starts making an enormous contribution to the impact. So if the desired striking point on a straight sword edge was about a third back from the tip, it wouldn’t ever have a large pommel.

Figure 13 - Illustration of a strike with a range of different
pommels. The front of the chart doesn't use a pommel, while the rear of the
chart uses a large pommel. There is no change for impacts at the pivot point,
relative to the pommel, but a large change near the tip.
|
|
|||
|
|
|||
|
|||